علاقة غير خطية لحل مشكلة XOR
تشرح هذه المقالة استخدام الشبكات العصبية غير الخطية لحل مشكلة XOR ، وطريقة تهيئة المعلمة ، وسبب استخدام CrossEntropy بدلاً من MSE في مشاكل التصنيف.
أولاً ، الحل الطبيعي لعلاقة XOR
استيراد numpy كـ np
استيراد matplotlib.pyplot كـ PLT
x_data = np.array ([[1،0،0] ،
[1،0،1] ،
[1،1،0] ،
[1،1،1]])
y_data = np.array ([[0]،
[1] ،
[1] ،
[0]])
# تهيئة الوزن ، نطاق القيمة هو -1 ~ 1
v = (np.random.random ([3،4]) - 0.5) * 2
w = (np.random.random ([4،1]) - 0.5) * 2
lr = 0.11
def السيني (x):
إرجاع 1 / (1 + np.exp (-x))
def d_sigmoid (x):
إرجاع x * (1-x)
تحديث def ():
x_data العالمية ، y_data ، w ، v ، lr ، L1 ، L2 ، L2_new
L1 = السيني (np.dot (x_data ، v)) # الناتج 4 * 4 مصفوفة الطبقة المخفية
L2 = السيني (np.dot (L1، w)) # الإخراج الفعلي للطبقة الناتجة 4 * 1
# احسب خطأ طبقة الإخراج والطبقة المخفية ، ثم ابحث عن مقدار التحديث
#
L2_delta = (L2-y_data) # y_data 4 * 1 مصفوفة
L1_delta = L2_delta.dot (wT) * d_sigmoid (L1)
# قم بتحديث الأوزان من طبقة الإدخال إلى الطبقة المخفية والأوزان من الطبقة المخفية إلى طبقة الإخراج
w_c = lr * L1.T.dot (L2_delta)
v_c = lr * x_data.T.dot (L1_delta)
ث = w-w_c
ت = ت- v_c
L2_new = softmax (L2)
def cross_entropy_error (y، t):
return -np.sum (t * np.log (y) + (1-t) * np.log (1-y))
def softmax (x):
exp_x = np.exp (x)
sum_exp_x = np.sum (exp_x)
y = exp_x / sum_exp_x
العودة ذ
إذا __name __ == '__ main__':
لأني في النطاق (1000):
update () #Update weights \
إذا كان i٪ 10 == 0:
مبعثر plt (i، np.mean (خطأ متقاطع (L2_new، y_data)))
plt.title ("منحنى الخطأ")
plt.xlabel ("التكرار")
plt.ylabel ("خطأ")
plt.show ()
طباعة (L2)
طباعة (cross_entropy_error (L2_new ، y_data))
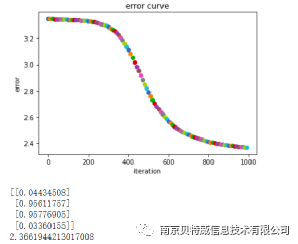
دعنا نتحدث عن بيانات الإدخال x أولاً: العمود الأول هو عنصر التحيز مضبوط دائمًا على 1 ، وآخر عمودين هما x1 ، x2 على التوالي. و y هو الناتج المقابل لـ x1 ، x2 ، أي تسمية نتيجة علاقة XOR. lr هو معدل التعلم المحدد. يتم حساب الخسارة عن طريق الانتروبيا المتقاطعة. أخيرًا ، يتم الحصول على نتيجة التنبؤ أسفل الرقم ، وليس من الصعب رؤية أن نتيجة التنبؤ لا تزال قريبة جدًا من الملصق .
2. استخدم علاقة خطية لحل مشكلة XOR
استيراد numpy كـ np
استيراد matplotlib.pyplot كـ PLT
x_data = np.array ([[1،0،0] ،
[1،0،1] ،
[1،1،0] ،
[1،1،1]])
y_data = np.array ([[0]،
[1] ،
[1] ،
[0]])
# تهيئة الوزن ، نطاق القيمة هو -1 ~ 1
v = (np.random.random ([3،4]) - 0.5) * 2
w = (np.random.random ([4،1]) - 0.5) * 2
lr = 0.11
تحديث def ():
x_data العالمية ، y_data ، w ، v ، lr ، L1 ، L2 ، L2_new
L1 = np.dot (x_data، v) # مصفوفة الإخراج 4 * 4 للطبقة المخفية
L2 = np.dot (L1، w) # الناتج الفعلي لطبقة المخرجات 4 * 1
# احسب خطأ طبقة الإخراج والطبقة المخفية ، ثم ابحث عن مقدار التحديث
#
L2_delta = (L2-y_data) # y_data 4 * 1 مصفوفة
L1_delta = L2_delta.dot (وزن)
# قم بتحديث الأوزان من طبقة الإدخال إلى الطبقة المخفية والأوزان من الطبقة المخفية إلى طبقة الإخراج
w_c = lr * L1.T.dot (L2_delta)
v_c = lr * x_data.T.dot (L1_delta)
ث = w-w_c
ت = ت- v_c
L2_new = softmax (L2)
def cross_entropy_error (y، t):
return -np.sum (t * np.log (y) + (1-t) * np.log (1-y))
def softmax (x):
exp_x = np.exp (x)
sum_exp_x = np.sum (exp_x)
y = exp_x / sum_exp_x
العودة ذ
إذا __name __ == '__ main__':
لأني في النطاق (300):
update () #update weights
إذا كان i٪ 10 == 0:
مبعثر plt (i، np.mean (خطأ متقاطع (L2_new، y_data)))
plt.title ("منحنى الخطأ")
plt.xlabel ("التكرار")
plt.ylabel ("خطأ")
plt.show ()
طباعة (L2)
print ("حجم الخطأ النهائي هو:"، cross_entropy_error (L2_new، y_data))
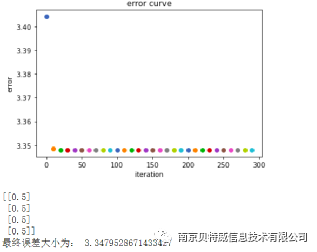
3. استخدم MSE كدالة خسارة لحل مشكلة XOR
استيراد numpy كـ np
استيراد matplotlib.pyplot كـ PLT
x_data = np.array ([[1،0،0] ،
[1،0،1] ،
[1،1،0] ،
[1،1،1]])
y_data = np.array ([[0]،
[1] ،
[1] ،
[0]])
# تهيئة الوزن ، نطاق القيمة هو -1 ~ 1
v = (np.random.random ([3،4]) - 0.5) * 2
w = (np.random.random ([4،1]) - 0.5) * 2
lr = 0.11
def السيني (x):
إرجاع 1 / (1 + np.exp (-x))
def d_sigmoid (x):
إرجاع x * (1-x)
تحديث def ():
x_data العالمية ، y_data ، w ، v ، lr ، L1 ، L2 ، L2_new
L1 = السيني (np.dot (x_data ، v)) # الناتج 4 * 4 مصفوفة الطبقة المخفية
L2 = السيني (np.dot (L1، w)) # الإخراج الفعلي للطبقة الناتجة 4 * 1
#
L2_delta = (L2-y_data) * d_sigmoid (L2) # y_data 4 * 1 مصفوفة
L1_delta = L2_delta.dot (wT) * d_sigmoid (L1)
# قم بتحديث الأوزان من طبقة الإدخال إلى الطبقة المخفية والأوزان من الطبقة المخفية إلى طبقة الإخراج
w_c = lr * L1.T.dot (L2_delta)
v_c = lr * x_data.T.dot (L1_delta)
ث = w-w_c
ت = ت- v_c
L2_new = softmax (L2)
def softmax (x):
exp_x = np.exp (x)
sum_exp_x = np.sum (exp_x)
y = exp_x / sum_exp_x
العودة ذ
إذا __name __ == '__ main__':
لأني في النطاق (1000):
update () #Update weights \
إذا كان i٪ 10 == 0:
مبعثر plt (i، np.mean ((y_data-L2) ** 2) / 2)
plt.title ("منحنى الخطأ")
plt.xlabel ("التكرار")
plt.ylabel ("خطأ")
plt.show ()
طباعة (L2)
طباعة (np.mean (((y_data-L2) ** 2) / 2))
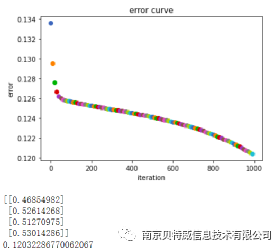
ليس من الصعب أن نرى أن استخدام MSE لا يمكن أن يحل مشكلة XOR ، فما السبب؟
من الناحية النظرية ، سيكون من الممكن استخدام دالة الخسارة التربيعية لمشاكل التصنيف أيضًا ، ولكنها غير مناسبة. أولاً ، إن تقليل دالة الخسارة التربيعية إلى أدنى حد يكافئ أساسًا تقدير الاحتمال الأقصى في ظل افتراض أن الخطأ يتبع توزيعًا غاوسيًا ، في حين أن معظم مشاكل التصنيف ليس لها توزيع غاوسي. علاوة على ذلك ، في التطبيقات العملية ، يمكن أن يؤدي الانتروبيا المتقاطعة ، جنبًا إلى جنب مع وظيفة تنشيط Softmax ، إلى زيادة قيمة الخسارة ، وكلما زاد حجم المشتق ، وصغر قيمة الخسارة ، كلما كان المشتق أصغر ، والذي يمكنه تسريع معدل التعلم . ومع ذلك ، إذا تم استخدام دالة الخسارة التربيعية ، فكلما زادت الخسارة ، كان المشتق أصغر ، ويكون معدل التعلم بطيئًا للغاية. انظر إلى الصورة أدناه لترى المشكلة.
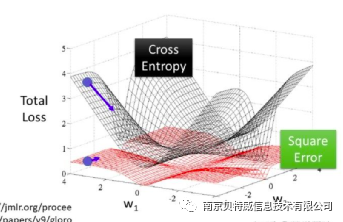
انظر إلى الرسم البياني للنتيجة الأول أعلاه والرسم البياني لنتيجة الفصل الثالث:



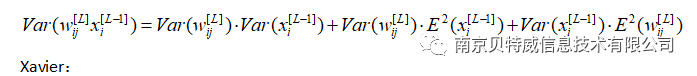
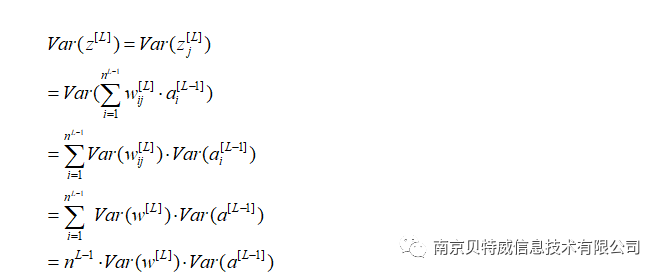
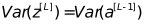
ثم تحتاج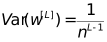
في backpropagation ، نفس الشيء
بحاجة إلى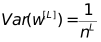
خذ المتوسط التوافقي لهذين الرقمين: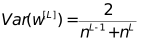
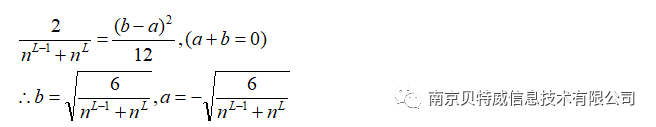
(أ ، ب) هو نطاق الأوزان الأولية.
في هذا المثال ، عدد الخلايا العصبية في الطبقة المخفية هو 4 ، لذلك يمكن ضبط نطاق تهيئة الوزن تقريبًا على (-1،1).