👇 Lianxh Club Tweet Navigation | www.lianxh.cn

-
🍎 Stata: أساسيات Stata | رسم Stata | برامج Stata | أوامر Stata الجديدة -
📘 الأوراق: معالجة البيانات | إخراج النتائج | كتابة الورق | مشاركة البيانات -
💹 المقاييس: تحليل الانحدار | تكييف التقاطع | IV-GMM | السلاسل الزمنية | بيانات اللوحة | المقاييس المكانية | لوغاريتم الاحتمالات | الانحدار الكمي -
⛳ الموضوع: SFA-DEA | تحليل البقاء | الزاحف | التعلم الآلي | تحليل النص -
🔃 السببية: اضطراب الشخصية الانفصامية | RDD | الاستدلال السببي | طريقة التحكم الاصطناعية | مطابقة PSM -
🔨 الأدوات: الأدوات | Markdown | Python-R-Stata -
🎧 دورة تدريبية: Open Class-Live | موضوعات المترولوجيا | حول Lianxianghui

Lianxianghui 2022 موضوع خاص عن القياس المكاني

المؤلف : Liang Shuzhen (جامعة Huaqiao)
البريد الإلكتروني : [email protected]
ملاحظة المحرر : تم تجميع هذه المقالة بشكل أساسي من "تشابه Jaccard ومسافة Jaccard في Python" ، شكرًا لك!
تذكير: لا يتم تفعيل الرابط الموجود في النص في WeChat. الرجاء النقر فوق "قراءة النص الأصلي" في الجزء السفلي . أو اضغط مطولاً / امسح رمز الاستجابة السريعة التالي مباشرةً للانتقال مباشرةً إلى النص الأصلي:

جدول المحتويات
-
1 المقدمة
-
2. تعريف تشابه Jaccard
-
3. حساب تشابه Jaccard
-
4. تعريف مسافة الجاكارد
-
5. حساب مسافة الجاكارد
-
6. التشابه والمسافة بين المتغيرات الثنائية غير المتماثلة
-
7. بايثون تحسب تشابه Jaccard
-
8. بيثون حساب مسافة الجاكارد
-
9. تحسب بايثون المتغيرات الثنائية غير المتماثلة
-
10. بايثون تحسب تشابه Jaccard الصينية
-
11. التغريدات ذات الصلة
1 المقدمة
يستخدم تشابه Jaccard على نطاق واسع في حساب التشابه بين البيانات ، مثل تشابه المجموعة وتشابه النص وما إلى ذلك. يحتاج مثيل Python في هذه المقالة إلى استخدام ثلاث وحدات scipy، و. أوامر التثبيت المحددة هي كما يلي:sklearnnumpy
pip install scipy
pip install sklearn
pip install numpy
2. تعريف تشابه Jaccard
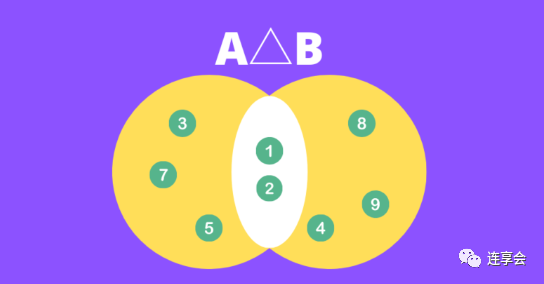
تشابه Jaccard (المعروف أيضًا باسم معامل تشابه Jaccard ، أو مؤشر Jaccard) هو إحصاء يستخدم لحساب التشابه بين مجموعتين ، ويمكن توسيعه ليشمل حساب تشابه النص. في Python ، يستخدم تشابه Jaccard بشكل أساسي لحساب التشابه بين مجموعتين أو المتغيرات الثنائية غير المتماثلة. رياضيا ، يمكن التعبير عن تشابه Jaccard كنسبة التقاطع والاتحاد. خذ المجموعة أ واضبط ب كمثال:

صيغة حساب تشابه Jaccard هي:
جزء البسط من الصيغة هو تقاطع المجموعتين ، كما هو موضح في الجزء الأصفر من الشكل التالي:
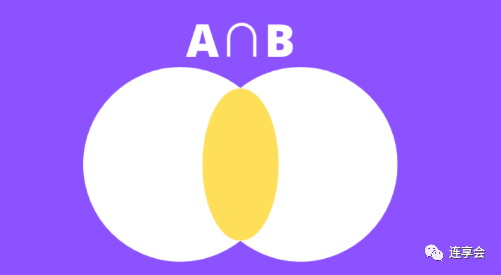
الجزء المقام في الصيغة هو اتحاد المجموعتين ، كما هو موضح في الجزء الأصفر من الشكل التالي:

رياضياً ، يمكن فهم تشابه Jaccard على أنه نسبة عدد عناصر التقاطع إلى عدد عناصر الاتحاد في الشكل أعلاه ، على وجه التحديد:
-
إذا كانت المجموعتان متساويتين ، مثل و ، فإن تشابه Jaccard هو 1 ؛ -
إذا كان عنصرا المجموعة مختلفين تمامًا ، مثل و ، فإن تشابه Jaccard هو 0 ؛ -
يكون تشابه Jaccard بين 0 و 1 إذا كانت المجموعتان تحتويان على بعض العناصر نفسها ، على سبيل المثال و .
3. حساب تشابه Jaccard
ضع في اعتبارك المجموعتين التاليتين: و ، والتي يمكن تمثيلها في الرسم البياني على النحو التالي:

الخطوة 1: ابحث عن تقاطع المجموعتين. في هذا المثال ، .
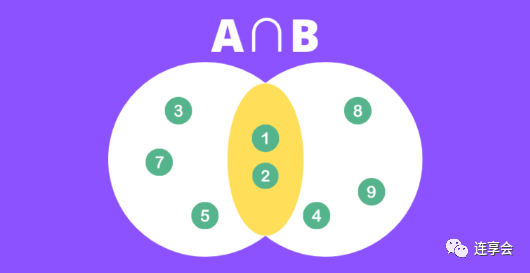
الخطوة 2 : ابحث عن اتحاد المجموعتين. في هذا المثال ، .
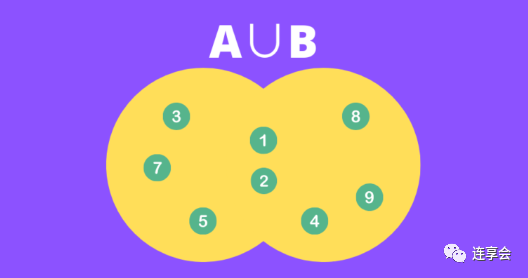
الخطوة 3 : احسب النسبة.
4. تعريف مسافة الجاكارد
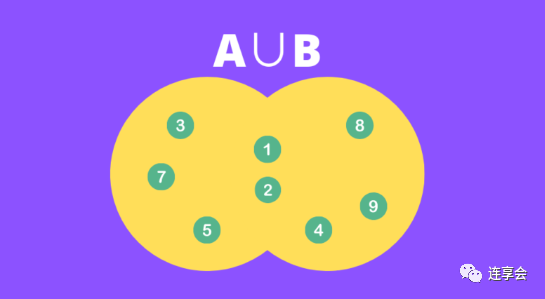
على عكس تشابه Jaccard ، تقيس مسافة Jaccard مدى اختلاف مجموعتين. رياضيا ، يمكن التعبير عنها كنسبة من المكمل لاتحاد التقاطع. خذ أيضًا المجموعة A والمجموعة B كمثال:

صيغة مسافة Jaccard هي:
يمكن أيضًا التعبير عن بسط مسافة Jaccard على النحو التالي:
يمكن فهمه بشكل حدسي على أنه الفرق بين المجموعتين ، كما هو موضح في الجزء الأصفر من الشكل التالي:
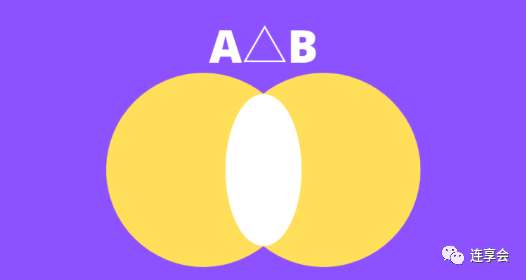
مقام مسافة Jaccard هو نفسه تشابه Jaccard ، وهو اتحاد المجموعتين.

رياضياً ، يمكن فهم مسافة Jaccard على أنها نسبة عدد عناصر الفرق المحددة إلى عدد عناصر الاتحاد. خاصة:
-
إذا كانت المجموعتان متساويتين ، مثل و ، فإن مسافة Jaccard هي 0 ؛ -
إذا كان عنصرا مجموعة مختلفين تمامًا ، مثل و ، فإن مسافة Jaccard هي 1 ؛ -
إذا كانت مجموعتان تحتويان على عناصر متطابقة جزئيًا ، مثل و ، فإن مسافة Jaccard تكون بين 0 و 1.
5. حساب مسافة الجاكارد
ضع في اعتبارك المجموعتين التاليتين: و ، والتي يمكن تمثيلها في الرسم البياني على النحو التالي:

الخطوة 1: ابحث عن مكمل تقاطع المجموعتين.
الخطوة 2 : ابحث عن اتحاد المجموعتين. في هذا المثال ، .
الخطوة 3 : احسب النسبة.
6. التشابه والمسافة بين المتغيرات الثنائية غير المتماثلة
سيناقش هذا القسم التطبيق المحدد لتشابه Jaccard ومسافة Jaccard للمتغيرات الثنائية غير المتماثلة.
المتغير الثنائي ، كما يوحي الاسم ، يحتوي على فئتين أو حالتين فقط. عندما تكون القيمة 0 ، فهذا يعني أن الحالة لا تظهر ؛ عندما تكون القيمة 1 ، فهذا يعني أن الحالة تظهر. على سبيل المثال ، يمثل المدخن كائنًا مريضًا ، ويعني 1 أن المريض يدخن ، ويعني 0 أن المريض لا يدخن. إذا كان متغيرًا ثنائيًا متماثلًا ، فإن سمتين لهما نفس الوزن ، أي الحالات المختلفة يتم ترميزها بـ 0 أو 1 وليس لها أي تفضيل (على سبيل المثال ، يتم ترميز 0 و 1 لمتغير الجنس).
نتيجتا المتغيرات الثنائية غير المتماثلة لها أهمية مختلفة. على سبيل المثال ، يتم تقسيم نتائج اختبار الحمض النووي إلى إيجابية وسلبية ، ويتم ترميز النتائج الإيجابية بالرقم 1 (الاحتمال أقل ، والنتيجة أكثر أهمية) ، والنتائج السلبية يتم ترميزها بالرقم 0. بالنظر إلى كائنين متغيرين ثنائيين غير متماثلين ، فإن الحالة التي يأخذ فيها كلا الكائنين 1 هي أكثر أهمية وذات مغزى من الحالة التي يأخذ فيها كلا الكائنين 0.
بافتراض وجود متجهين من الأبعاد n A و B ، فإن صيغة حساب تشابه Jaccard هي:
صيغة حساب مسافة Jaccard هي:
في،
-
يمثل عدد اثنين من المتجهات التي تكون المكونات المقابلة لها كلاهما 1 ؛ -
يمثل عدد المكونات المقابلة للمتجهين 0 و 1 ؛ -
يمثل عدد المكونات المقابلة للمتجهين 1 و 0 ؛ -
يمثل عدد متجهين يكون كلا المكونين المتناظرين فيهما 0.
و .
نحن نفهمها من خلال حالة بسيطة. على سبيل المثال ، يبيع المتجر 6 أنواع من السلع (التفاح ، والطماطم ، والبيض ، والحليب ، والقهوة ، والسكر) ، ويوجد سجلا شراء للعملاء:
-
الزبون "أ" يشتري: التفاح والحليب والقهوة -
يشتري العميل "ب": البيض والحليب والقهوة
من المعلومات الواردة أعلاه ، يمكن إنشاء المصفوفة التالية:
| تفاحة | طماطم | بيض | لبن | قهوة | سكر | |
|---|---|---|---|---|---|---|
| أ | 1 | 0 | 0 | 1 | 1 | 1 |
| ب | 0 | 0 | 1 | 1 | 1 | 0 |
لكل سلعة ، قرار الشراء هو متغير ثنائي ، 1 للشراء و 0 لعدم الشراء. بعد ذلك ، نحسب تشابه Jaccard ومسافة Jaccard في خطوتين:
الخطوة 1: أوجد قيمة M.
| كمية | يبين | |
|---|---|---|
| (م_ {11}) | 2 | اشترى كل من A و B الحليب والقهوة |
| (M_ {01}) | 1 | اشترى ب البيض لم يشتروا البيض |
| (م_ {10}) | 2 | اشترى A التفاح والسكر ، لكن B لم يفعل |
| (M_ {00}) | 1 | لم يشترِ أي من "أ" ولا "ب" الطماطم |
وهو نفس عدد المنتجات ويتم التحقق منه .
الخطوة 2 : استبدل الصيغة ، ثم
-
تشابه الجاكارد:
-
مسافة الجاكارد:
7. بايثون تحسب تشابه Jaccard
حدد مجموعتين في بايثون:
A = {1, 2, 3, 5, 7}
B = {1, 2, 4, 8, 9}
تحسب وظيفة البناء تشابه Jaccard ، وتمرير المجموعة A وتعيين B كمعلمات للوظيفة:
def jaccard_similarity(A, B):
# 求集合 A 和集合 B 的交集
nominator = A.intersection(B)
# 求集合 A 和集合 B 的并集
denominator = A.union(B)
# 计算比率
similarity = len(nominator)/len(denominator)
return similarity
similarity = jaccard_similarity(A, B)
print(similarity)
تكون النتيجة 0.25 ، وهي نفس النتيجة المحسوبة يدويًا.
8. بيثون حساب مسافة الجاكارد
احسب مسافة Jaccard باستخدام نفس البيانات:
def jaccard_distance(A, B):
#Find symmetric difference of two sets
nominator = A.symmetric_difference(B)
#Find union of two sets
denominator = A.union(B)
#Take the ratio of sizes
distance = len(nominator)/len(denominator)
return distance
distance = jaccard_distance(A, B)
print(distance)
تكون النتيجة 0.75 ، وهي نفس النتيجة المحسوبة يدويًا.
9. تحسب بايثون المتغيرات الثنائية غير المتماثلة
# 导入模块
import numpy as np
from scipy.spatial.distance import jaccard
from sklearn.metrics import jaccard_score
قم بإنشاء متجهين من المصفوفة:
| تفاحة | طماطم | بيض | لبن | قهوة | سكر | |
|---|---|---|---|---|---|---|
| أ | 1 | 0 | 0 | 1 | 1 | 1 |
| ب | 0 | 0 | 1 | 1 | 1 | 0 |
A = np.array([1,0,0,1,1,1])
B = np.array([0,0,1,1,1,0])
similarity = jaccard_score(A, B)
distance = jaccard(A, B)
print(f'Jaccard similarity is equal to: {similarity}')
print(f'Jaccard distance is equal to: {distance}')
النتيجة التي تم الحصول عليها هي:
Jaccard similarity is equal to: 0.4
Jaccard distance is equal to: 0.6
10. بايثون تحسب تشابه Jaccard الصينية
import pandas as pd
import jieba
import re
# 调用数据
data = pd.read_excel("https://file.lianxh.cn/data/m/mda.xlsx")
stopwords = pd.read_csv("https://file.lianxh.cn/data/c/cn_stopwords.txt", names=["stopwords"])
# 定义分词函数def cut_words(text):
def cut_words(text):
words_list = []
text = re.sub("[\W\d]", "", text) # 替换符号和数字
words = jieba.lcut(text)
for word in words:
if word not in list(stopwords["stopwords"]):
words_list.append(word)
return" ".join(words_list)
# 对文本分词
data["BusDA"] = data["BusDA"].apply(cut_words)
data
# 定义 jaccard 相似度函数
def jaccard_similarity(list1, list2):
s1 = set(list1)
s2 = set(list2)
return float(len(s1.intersection(s2)) / len(s1.union(s2)))
jaccard_similarity(data["BusDA"][1], data["BusDA"][1])
11. التغريدات ذات الصلة
ملاحظة: أمر Stata الذي ينتج قائمة التغريدات التالية هو:
lianxh python, m
تثبيت أحدث إصدار منlianxhالأمر :
ssc install lianxh, replace
-
المواضيع: دورات المواضيع -
Stata + Python: الأسهم الزاحفة لتسجل ارتفاعات في تدفق مباشر -
الموضوع: مشاركة البيانات -
Python + Stata: كيفية الحصول على بيانات الصين التاريخية للأرصاد الجوية -
الموضوع: تحليل النص - الزاحف -
Python: احسب تشابه جيب التمام من أجل مناقشة الإدارة والتحليل -
Stata + Python: تزحف قائمة الأسهم بأعلى مستوياتها القياسية -
بايثون: تعليقات أسهم ثروة الشرقية الزاحفة لتحليل المشاعر -
القيمة المعرضة للمخاطر المعرضة للخطر: تطبيق Stata و Python -
دعم آلات المتجهات: تطبيق Stata و Python -
Python Crawler: تحليل النقاط الساخنة للبحث والموضوعات في البحث الاقتصادي -
الموضوع: Python-R-Matlab -
Stata + Python: أفكار جديدة لاستيراد مستندات Excel كبيرة - أخذ Guotai كمثال -
تفاعل Stata-Python-10: تكوين وتطبيق ميزات PyStata الجديدة لـ Stata17 -
Python:多进程、多线程及其爬虫应用 -
Python:爬取动态网站 -
Python爬取静态网站:以历史天气为例 -
Python:绘制动态地图-pyecharts -
Python爬虫1:小白系列之requests和json -
Python爬虫2:小白系列之requests和lxml -
Python爬虫:爬取华尔街日报的全部历史文章并翻译 -
Python爬虫:从SEC-EDGAR爬取股东治理数据-Shareholder-Activism -
Python:爬取巨潮网公告 -
Python:爬取上市公司公告-Wind-CSMAR -
Python: 6 小时爬完上交所和深交所的年报问询函 -
Python: 使用正则表达式从文本中定位并提取想要的内容

课程推荐:因果推断实用计量方法
主讲老师:邱嘉平教授
🍓 课程主页:https://gitee.com/lianxh/YGqjp


New! Stata 搜索神器:
lianxh和songblGIF 动图介绍
搜: 推文、数据分享、期刊论文、重现代码 ……
👉 安装:
. ssc install lianxh
. ssc install songbl
👉 使用:
. lianxh DID 倍分法
. songbl all

🍏 关于我们
-
连享会 ( www.lianxh.cn,推文列表) 由中山大学连玉君老师团队创办,定期分享实证分析经验。 -
直通车: 👉【百度一下: 连享会】即可直达连享会主页。亦可进一步添加 「知乎」,「b 站」,「面板数据」,「公开课」 等关键词细化搜索。
